第4回 リニアレギュレータってなに?(補足編)
2018年02月21日皆さんこんにちは、日清紡マイクロデバイスの講師Sです。さて第3回では許容損失について、第4回のDC/DCコンバータ (スイッチングレギュレータ) の中で詳細に説明することを予告していましたが、許容損失はリニアレギュレータにとっては非常に重要ですので、予定を変更して第4回もリニアレギュレータの補足編として、主にリニアレギュレータの効率と許容損失について説明したいと思います。
リニアレギュレータの効率
電源ICの効率
最初に、電源ICにおける効率について概説します。負荷デバイスが必要とする一定の電圧と電力を供給するのが電源ICの役割です。入力電源から供給される電力のすべてを負荷側に供給することができるのが理想の電源ICです。ただし電源ICは負荷デバイスに一定の電圧を供給するための制御に電力が必要になります。この電力が少ないことが「効率の良い電源」ということになります。
効率は電源ICの入力側から供給される電力のうち出力側の負荷デバイスで消費される電力の割合を指し、次の式で表されます。
効率は電源ICの性能を表す一つの指標になります。
リニアレギュレータ効率
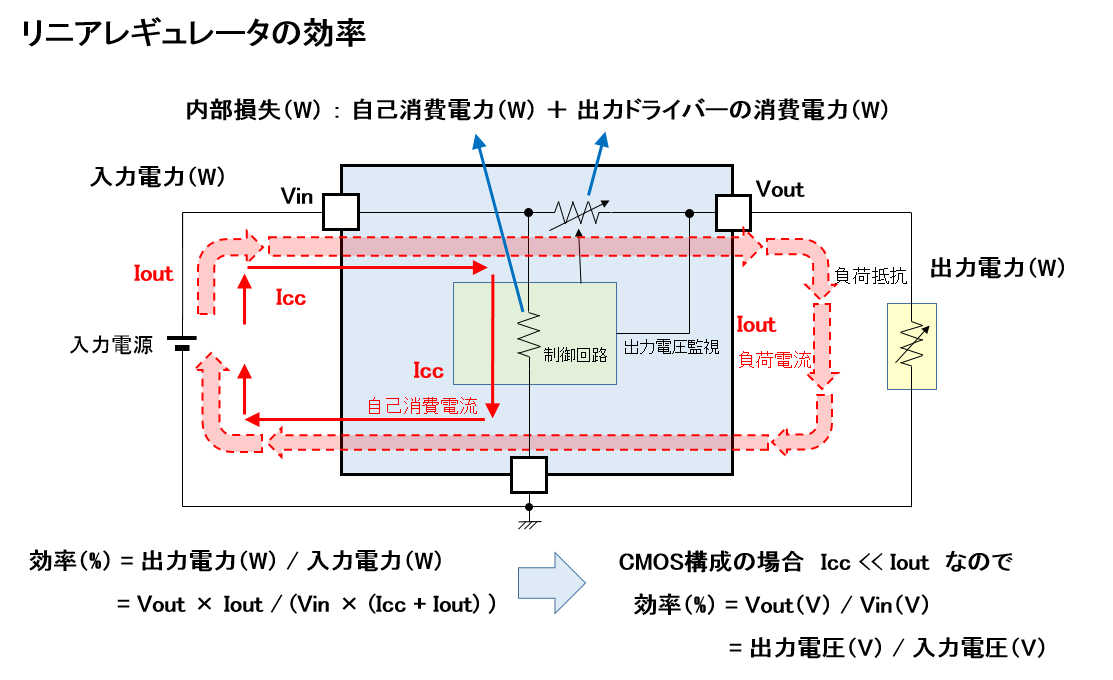
図1はリニアレギュレータのブロック図と各ブロックに流れる電流、各ブロックで消費される電力と、そこから導き出される効率を示しています。
リニアレギュレータに流れる電流は自己消費電流 Iccと出力に供給する負荷電流 Iout (出力電流) が加算されたものです。したがって、入力側から供給される入力電力は以下の式になります。
リニアレギュレータ内部で消費される電力 (内部損失) はレギュレータの制御回路等で消費される自己消費電力 (Vin × Icc) と出力ドライバで消費される電力 (Vin – Vout) × Ioutです。
したがって、内部損失は以下の式で表されます。
| 内部損失 (W) = Vin × Icc + (Vin – Vout) × Iout | ||
| Vin | : | 入力電圧 |
| Vout | : | 出力電圧 |
| Iout | : | 出力負荷電流 |
| Icc | : | 自己消費電流 |
また、出力電力 (W) は以下の式になります。
効率 (%) は出力電力 (W) / 入力電力 (W) ですので、以下の式で表されます。
CMOS構成のリニアレギュレータの場合は内部で消費する電流は非常に小さいので Icc << Iout として、内部で消費される電流を無視すれば効率は以下の式になります。
さらに分母分子で Iout が共通なので消去すると
として簡略化して表わすことができます。
リニアレギュレータは内部の出力ドライバトランジスタで電力を消費することで出力電圧を一定にしていますので効率の点では理想からかけ離れています。
| ※ 効率の点では次回の講座で予定しているDC/DCコンバータ (スイッチングレギュレータ) がすぐれています。リニアレギュレータとDC/DCコンバータの性能や特長の比較は次回以降で説明する予定です。 |
式からわかるように、入出力電位差を小さくできる用途ではドロップアウト電圧が非常に小さいLDOレギュレータを使うことで、DC/DCコンバータ並み、あるいはそれ以上の効率を実現することが可能です。例えばドロップアウト電圧が0.3VのLDOを入力電圧3.3V、出力電圧3.0Vの用途で使用すれば効率は91%となりDC/DCコンバータ並みの効率が実現可能です。
逆に入出力電位差が大きいと効率が悪くなりますが、この効率に寄与しない分が損失です。この損失分はすべて熱に変わるので、次にその熱の影響について考えたいと思います。
日清紡マイクロデバイス リニアレギュレータ製品の『★図研の回路モジュール無料ダウンロードサイト「Module Station」』はこちら!
リニアレギュレータの内部損失(消費電力)とパッケージの許容損失
許容損失とは一言で言うとIC内部で消費されて熱に変わる電力の許容値のことです。
もう少し説明を補足すると以下のようになります。
リニアレギュレータは内部の出力ドライバトランジスタで電力を消費することで出力電圧を一定にしていますが、この出力ドライバで消費される電力はすべて熱に変換されます。この発熱によってリニアレギュレータの温度が上昇しますが、リニアレギュレータ等の半導体デバイスチップが正常に動作することができる温度には上限があります。
この温度の上限を超えないために許容される内部損失(消費電力)の最大値が 『許容損失』 です。
それでは、許容損失がどのように導かれるかを、順を追って説明したいと思います。
熱抵抗
半導体チップ内部で消費される電力 (すなわち内部損失) はそれが熱源となってチップの温度を上昇させます。一方半導体チップはパッケージの中に実装されており、パッケージを通して放熱されますので、半導体チップの発熱量とパッケージの放熱量が均衡したところでチップの温度が決まります。
半導体チップの発熱量は個別のデバイスに依存するわけではなく消費電力 (内部損失) で決まります。また放熱特性はパッケージの種類や大きさ、実装する基板などによって決まります。
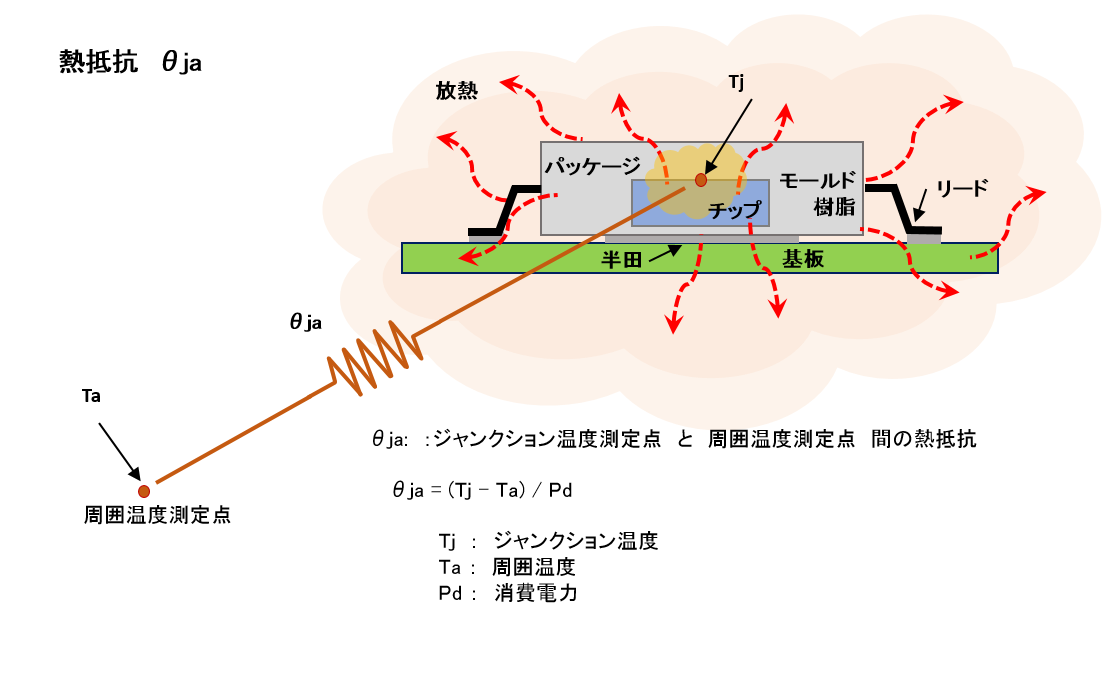
図2 はモールド樹脂パッケージに実装されたチップの表面で発生した熱が、モールド樹脂を経由してパッケージ表面から周囲へ放熱する場合やパッケージのリードフレームからリード、リードから実装基板に伝わり、実装基板から周囲へと放熱する場合等、あらゆる経路を伝わって放熱する様子を示しています。
パッケージの放熱特性が良いということは、チップの発熱箇所からパッケージの周囲へ熱が良く伝わるので、チップの発熱に対してチップの温度の上昇が小さいということです。逆に熱の伝わり方が悪いとチップの発熱に対してチップ温度の上昇が大きくなります。
すなわち、チップの発熱による温度上昇の大きさで熱の伝わりにくさを表せるということを示しています。これが熱抵抗の考え方です。
これを、式で表すと以下のようになります。
| θja = (Tj – Ta) / Pd | ||
| θja | : | ジャンクションと周辺温度測定点間の熱抵抗 |
| Tj | : | ジャンクション温度 |
| Ta | : | 周辺温度 |
| Pd | : | 消費電力 (内部損失) |
ここで添え字の『 j 』はJunction、『 a 』はAmbient です。
熱抵抗はパッケージから離れた地点 (パッケージの温度上昇が伝わらない地点) の温度 (周囲温度) を基準として半導体チップの電力消費 (内部損失) に対するジャンクション温度 (チップ温度) の上昇率で表すのが一般的です。
ところで熱抵抗の式は電気回路のオームの法則 R = V / I と同じと考えれば理解しやすいかも知れません。
※電気抵抗と熱抵抗の比較
・電気抵抗
電位の高いところから電位の低いところに向かってその電位差に比例する電流が流れます。
その比例係数が電気抵抗で、次の式で表されます。
電気抵抗 (Ω) = 電位差 (V) / 電流 (A)
・熱抵抗
温度の高いところから温度の低いところに向かってその温度差に比例する熱流が流れます。
その比例係数が熱抵抗であり、次の式で表されます。
熱抵抗 (℃/W) = 温度差 (℃) / 熱流 (W)
(注) 消費電力は1秒間の発熱量に相当しますので、消費電力に相当する熱量が熱抵抗を流れると考えます。
電流の流れにくさを示すのが電気抵抗であり、熱の伝わりにくさを示すのが熱抵抗です。
日清紡マイクロデバイス リニアレギュレータ製品の『★図研の回路モジュール無料ダウンロードサイト「Module Station」』はこちら!
ジャンクション温度の上限値(Tjmax)
次に半導体デバイスが正常に動作するためのジャンクション温度について考えます。
半導体製品が正常に動作することができる温度の上限値をジャンクション温度の最大値 (Tjmax) として規定しており、通常は125℃や150℃という値になります。
ジャンクション温度は半導体のPN接合部の温度ですが、半導体チップの温度と同じ意味で使われています。
パッケージの許容損失
1) 各パッケージにはそのパッケージとそれを実装する基板で決まる放熱特性を表す固有の熱抵抗があり、θja = (Tj – Ta) / Pd で表されることを示しました。
この式を Pdを求める式に書き換えると、以下の式になります。
2) 半導体製品が正常に動作することができる温度の上限値として、ジャンクション温度の最大値 (Tjmax) が決まっています。
この2つのことから、各パッケージにはそのパッケージに実装された半導体チップがジャンクション温度の最大値 (Tjmax) を超えないための消費電力 (内部損失) の上限値が決まります。
これがパッケージの許容損失 (Pdmax) であり、上記の式の Pd を Pdmax、Tj を Tjmaxに置き換えて以下の式で表わされます。
| Pdmax = (Tjmax – Ta) / θja | ||
| Pdmax | : | 許容損失 |
| Tjmax | : | ジャンクション温度の上限値 |
| Ta | : | 周囲温度 |
| θja | : | ジャンクション(温度)と周囲(温度)間の熱抵抗 |
以上のことをまとめると、パッケージの許容損失はそのパッケージに実装されるデバイス(ここでは電源ICであるリニアレギュレータ)が正常に動作するための消費電力(内部損失)の最大値であり、半導体製品ではジャンクション温度の最大値(Tjmax)を超えないための消費電力(内部損失)の上限値ということです。
許容損失データの事例
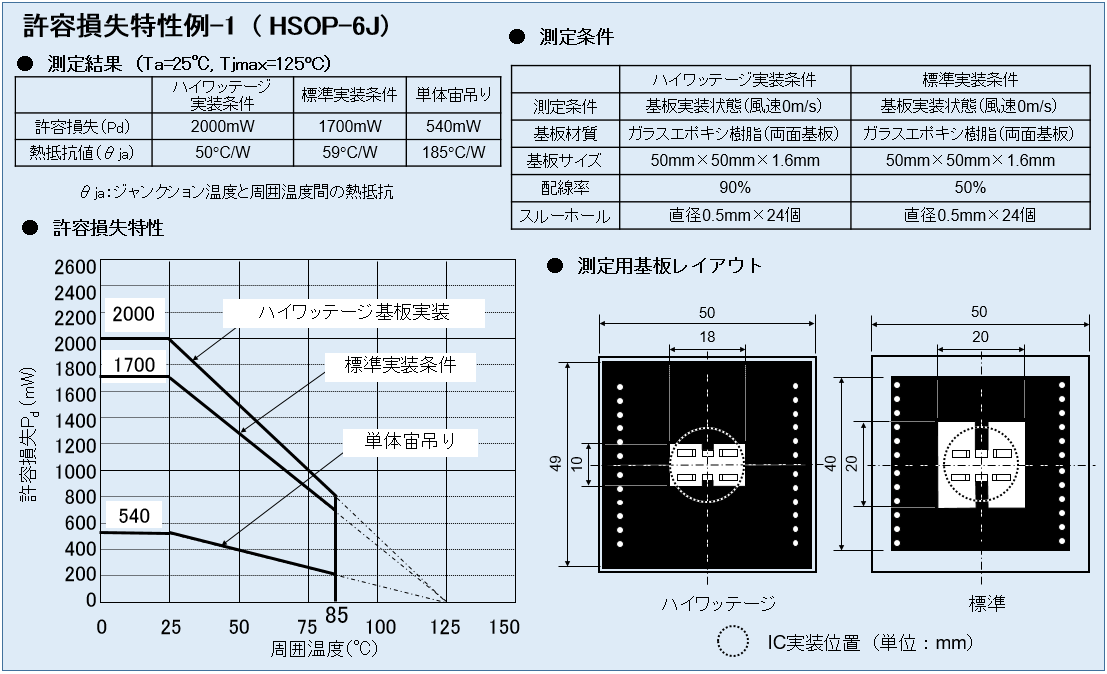
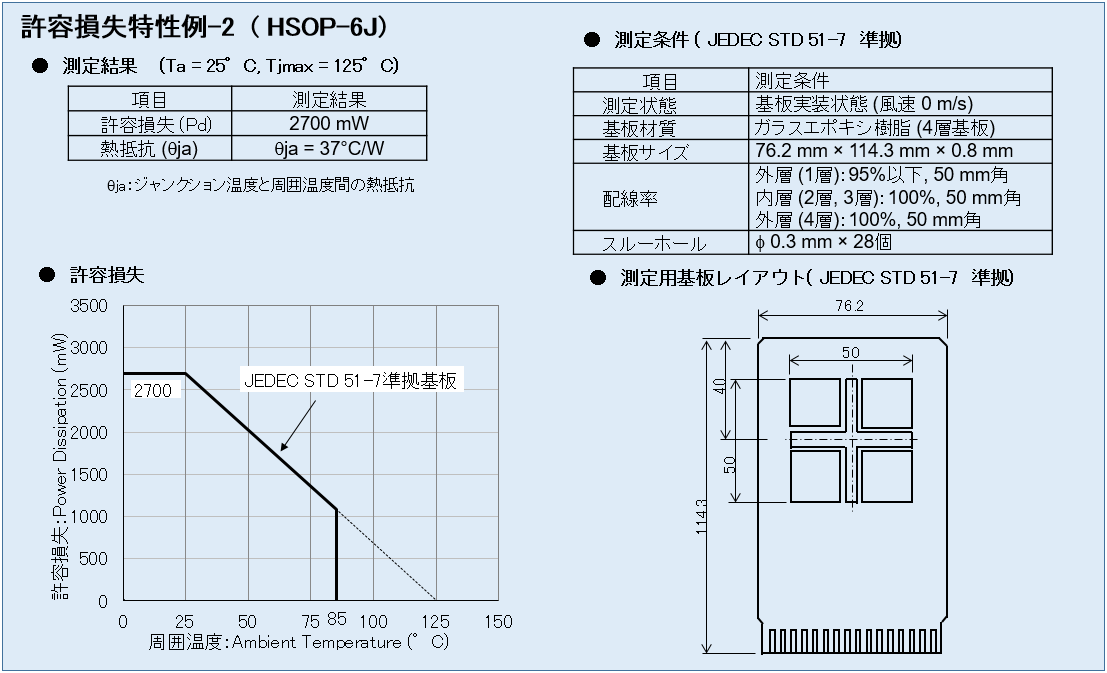
図3-1、3-2に特定の基板に実装されたパッケージの熱抵抗とTjmax = 125℃とした場合の周囲温度25℃での許容損失のデータ、また許容損失と周囲温度との関係を示すグラフの一例を示します。
図3-1 には基板に実装しない場合、配線率が 90%と 50%の2層両面基板に実装された場合の計3つの条件での熱抵抗と、許容損失のデータを示しています。また図3-2 にはさらに実装基板を4層にして、より配線率を高めた場合の熱抵抗と許容損失のデータが示されています。
これらのデータから同じパッケージでも実装される基板によって熱抵抗、許容損失が大きく変わることがわかります。また実装基板の配線率を高くし基板の配線層数を増やすことで、熱抵抗が下がり許容損失が高くなることがわかります。
ここで強調しておきたいのは、図3-1、3-2の説明で示したようにパッケージ毎に記載されている熱抵抗や許容損失は特定の条件下での測定結果であるということです。
基板のレイアウトパターン、配線密度が変われば、熱抵抗の値が変わり、許容損失も変化します。データシート等に記載された数値はあくまで参考値として考える必要があります。
実際の製品の基板に実装した場合の許容損失は、その基板を使って評価した熱抵抗から計算する必要があります。詳細は我々メーカーに相談されるのがよいでしょう。
許容損失と入出力電位差
『リニアレギュレータの効率』の項でレギュレータの内部損失Pdは以下の式になることを示しました。
CMOS構成のリニアレギュレータでは、許容損失を議論するような出力電流が非常に大きい範囲では自己消費電流は無視できますので、内部損失は以下の式になります。
許容損失の式を再度記載します。
これらの式の関係性を充分考慮してリニアレギュレータ製品やパッケージを選択する必要があります。
おわりに
今回は、リニアレギュレータにとって許容損失が非常に重要ですので、1回分の紙面を割いて説明しました。
次回はDC/DCコンバータ(スイッチングレギュレータ)の第1回目を予定しています。
最後まで読んでいただきありがとうございました。
他の「おしえて電源IC」連載記事
第1回 電源ICってなに?
第2回 リニアレギュレータってなに?(前編)
第3回 リニアレギュレータってなに?(後編)
第4回 リニアレギュレータってなに?(補足編)
第5回 DC/DCコンバータってなに?(その1)
第6回 DC/DCコンバータってなに?(その2)
第7回 DC/DCコンバータってなに?(その3)
第8回 DC/DCコンバータってなに?(その4)
第9回 DC/DCコンバータってなに?(その5)
第10回 電源監視ICってなに?(その1)
第11回 電源監視ICってなに?(その2)
第12回 リチウムイオン電池保護ICってなに?(その1)
第13回 リチウムイオン電池保護ICってなに?(その2)
第14回 スイッチICってなに?
第15回 複合電源IC(PMIC)ってなに?
★図研の回路モジュール無料ダウンロードサイト「Module Station」
<電源>
DC-DC 公開中
リニアレギュレータ 公開中
<複合電源>
複合電源 公開中
<電源管理・システム管理>
Liイオン電池保護 4月末 公開予定
パワースイッチ 公開中
電圧検出リセット 公開中
ウォッチドッグタイマ 公開中
<タイミング>
リアルタイムクロック 公開中
<LEDドライバ>
DC入力タイプ 公開中
★日清紡マイクロデバイスサイトの技術ページ
| リニアレギュレータ | 民生用 |
| 産業用 | |
| 車載用 |
| DC/DCコンバータ | 民生用 |
| 産業用 | |
| 車載用 |
| 電源監視IC | リセットIC |
| ウォッチドッグタイマ | |
| リセットタイマ |
| リチウムイオン電池用保護IC |
| スイッチIC |
| 複合電源IC |
日清紡マイクロデバイス 技術・サポート
 | 執筆者プロフィール 講師S (日清紡マイクロデバイス株式会社 設計センター 設計技術部) 入社以来長期に渡り、ゲートアレイ・マイコン・メモリ・電源ICなどアナログ・デジタルの各種設計に携わる。その後、複合電源ICのテスト技術も極める~設計・テスティングとその教育のスペシャリスト。毎年入社してくる技術者の卵に対する、聞き手目線の優しい解説と丁寧な指導は社内でも有名。その実績を買われ、現在はシニアエンジニアとして後進の育成や新規技術の相談役として活躍中。 日清紡マイクロデバイス株式会社について 世界に先駆けて製品化を実現したCMOSアナログ技術をコアとして、携帯機器市場向けには小型・低消費電力の電源ICを、車載・産機市場向けには高耐圧・大電流・高性能を特長とした電源ICを、Liイオンバッテリ市場向けには小型で高精度な保護ICを提供し、お客様製品の付加価値向上に貢献しています。 日清紡マイクロデバイス公式サイトはこちら |